[Chapter Sixteen][Previous]
[Next] [Art of
Assembly][Randall Hyde]
Art of Assembly: Chapter Sixteen
- 16.8 - Some Sample Pattern Matching Applications
- 16.8.1 - Converting Written Numbers to
Integers
16.8 Some Sample Pattern Matching Applications
The best way to learn how to convert a pattern matching problem to the
respective pattern matching algorithms is by example. The following sections
provide several examples of some small pattern matching problems and their
solutions.
16.8.1 Converting Written Numbers to Integers
One interesting pattern matching problem is to convert written (English)
numbers to their integer equivalents. For example, take the string "one
hundred ninety-two" and convert it to the integer 192. Although written
numbers represent a pattern quite a bit more complex than the ones we've
seen thus far, a little study will show that it is easy to decompose such
strings.
The first thing we will need to do is enumerate the English words we will
need to process written numbers. This includes the following words:
zero, one, two, three, four, five, six, seven, eight, nine, ten, eleven
twelve, thirteen, fourteen, fifteen, sixteen, seventeen, eighteen, nineteen,
twenty, thirty, forty, fifty sixty, seventy, eighty, ninety, hundred, and
thousand.
With this set of words we can build all the values between zero and 65,535
(the values we can represent in a 16 bit integer.
Next, we've got to decide how to put these words together to form all the
values between zero and 65,535. The first thing to note is that zero only
occurs by itself, it is never part of another number. So our first production
takes the form:
Number  zero | NonZero
zero | NonZero
The next thing to note is that certain values may occur in pairs,
denoting addition. For example, eighty-five denotes the sum of eighty plus
five. Also note that certain other pairs denote multiplication. If you have
a statement like "two hundred" or "fifteen hundred"
the "hundred" word says multiply the preceding value by 100.
The multiplicative words, "hundred" and "thousand" ,
are also additive. Any value following these terms is added in to the total;
e.g., "one hundred five" means 1*100+5. By combining the appropriate
rules, we obtain the following grammar
NonZero  Thousands Maybe100s | Hundreds
Thousands
Thousands Maybe100s | Hundreds
Thousands  Under100 thousand
Maybe100s
Under100 thousand
Maybe100s  Hundreds |
Hundreds | 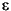 Hundreds
Hundreds  Under100 hundred After100 | Under100
After100
Under100 hundred After100 | Under100
After100  Under100 |
Under100 | 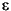 Under100
Under100  Tens Maybe1s| Teens | ones
Maybe1s
Tens Maybe1s| Teens | ones
Maybe1s  Ones |
Ones | 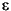 ones
ones  one | two | three | four | five | six | seven | eight | nine
teens
one | two | three | four | five | six | seven | eight | nine
teens  ten | eleven | twelve | thirteen | fourteen | fifteen | sixteen |
seventeen | eighteen | nineteen
tens
ten | eleven | twelve | thirteen | fourteen | fifteen | sixteen |
seventeen | eighteen | nineteen
tens  twenty | thirty | forty | fifty | sixty | seventy | eighty | ninety
twenty | thirty | forty | fifty | sixty | seventy | eighty | ninety
The final step is to add semantic actions to actually convert the strings
matched by this grammar to integer values. The basic idea is to initialize
an accumulator value to zero. Whenever you encounter one of the strings
that ones, teens, or tens matches, you add the corresponding value to the
accumulator. If you encounter the hundred or thousand strings, you multiply
the accumulator by the appropriate factor. The complete program to do the
conversion follows:
; Numbers.asm
;
; This program converts written English numbers in the range "zero"
; to "sixty five thousand five hundred thirty five" to the corresponding
; integer value.
.xlist
include stdlib.a
includelib stdlib.lib
matchfuncs
.list
dseg segment para public 'data'
Value word 0 ;Store results here.
HundredsVal word 0
ThousandsVal word 0
Str0 byte "twenty one",0
Str1 byte "nineteen hundred thirty-five",0
Str2 byte "thirty three thousand two hundred nineteen",0
Str3 byte "three",0
Str4 byte "fourteen",0
Str5 byte "fifty two",0
Str6 byte "seven hundred",0
Str7 byte "two thousand seven",0
Str8 byte "four thousand ninety six",0
Str9 byte "five hundred twelve",0
Str10 byte "twenty three thousand two hundred ninety-five",0
Str11 byte "seventy-five hundred",0
Str12 byte "sixty-five thousand",0
Str13 byte "one thousand",0
; The following grammar is what we use to process the numbers.
; Semantic actions appear in the braces.
;
; Note: begin by initializing Value, HundredsVal, and ThousandsVal to zero.
;
; N -> separators zero
; | N4
;
; N4 -> do1000s maybe100s
; | do100s
;
; Maybe100s -> do100s
; | <empty string>
;
; do1000s -> Under100 "THOUSAND" separators
; {ThousandsVal := Value*1000}
;
; do100s -> Under100 "HUNDRED"
; {HundredsVal := Value*100} After100
; | Under100
;
; After100 -> {Value := 0} Under100
; | {Value := 0} <empty string>
;
; Under100 -> {Value := 0} try20 try1s
; | {Value := 0} doTeens
; | {Value := 0} do1s
;
; try1s -> do1s | <empty string>
;
; try20 -> "TWENTY" {Value := Value + 20}
; | "THIRTY" {Value := Value + 30}
; | ...
; | "NINETY" {Value := Value + 90}
;
; doTeens -> "TEN" {Value := Value + 10}
; | "ELEVEN" {Value := Value + 11}
; | ...
; | "NINETEEN" {Value := Value + 19}
;
; do1s -> "ONE" {Value := Value + 1}
; | "TWO" {Value := Value + 2}
; | ...
; | "NINE" {Value := Value + 9}
separators pattern {anycset, delimiters, 0, delim2}
delim2 pattern {spancset, delimiters}
doSuccess pattern {succeed}
AtLast pattern {sl_match2, separators, AtEOS, AtEOS}
AtEOS pattern {EOS}
N pattern {sl_match2, separators, N2, N2}
N2 pattern {matchistr, zero, N3, AtLast}
zero byte "ZERO",0
N3 pattern {sl_match2, N4, 0, AtLast}
N4 pattern {sl_match2, do1000s, do100s, Maybe100s}
Maybe100s pattern {sl_match2, do100s, AtLast, AtLast}
do1000s pattern {sl_match2, Under100, 0, do1000s2}
do1000s2 pattern {matchistr, str1000, 0, do1000s3}
do1000s3 pattern {sl_match2, separators, do1000s4, do1000s5}
do1000s4 pattern {EOS, 0, 0, do1000s5}
do1000s5 pattern {Get1000s}
str1000 byte "THOUSAND",0
do100s pattern {sl_match2, do100s1, Under100, After100}
do100s1 pattern {sl_match2, Under100, 0, do100s2}
do100s2 pattern {matchistr, str100, 0, do100s3}
do100s3 pattern {sl_match2, separators, do100s4, do100s5}
do100s4 pattern {EOS, 0, 0, do100s5}
do100s5 pattern {Get100s}
str100 byte "HUNDRED",0
After100 pattern {SetVal, 0, 0, After100a}
After100a pattern {sl_match2, Under100, doSuccess}
Under100 pattern {SetVal, 0, 0, Under100a}
Under100a pattern {sl_match2, try20, Under100b, Do1orE}
Under100b pattern {sl_match2, doTeens, do1s}
Do1orE pattern {sl_match2, do1s, doSuccess, 0}
NumPat macro lbl, next, Constant, string
local try, SkipSpcs, val, str, tryEOS
lbl pattern {sl_match2, try, next}
try pattern {matchistr, str, 0, SkipSpcs}
SkipSpcs pattern {sl_match2, separators, tryEOS, val}
tryEOS pattern {EOS, 0, 0, val}
val pattern {AddVal, Constant}
str byte string
byte 0
endm
NumPat doTeens, try11, 10, "TEN"
NumPat try11, try12, 11, "ELEVEN"
NumPat try12, try13, 12, "TWELVE"
NumPat try13, try14, 13, "THIRTEEN"
NumPat try14, try15, 14, "FOURTEEN"
NumPat try15, try16, 15, "FIFTEEN"
NumPat try16, try17, 16, "SIXTEEN"
NumPat try17, try18, 17, "SEVENTEEN"
NumPat try18, try19, 18, "EIGHTEEN"
NumPat try19, 0, 19, "NINETEEN"
NumPat do1s, try2, 1, "ONE"
NumPat try2, try3, 2, "TWO"
NumPat try3, try4, 3, "THREE"
NumPat try4, try5, 4, "FOUR"
NumPat try5, try6, 5, "FIVE"
NumPat try6, try7, 6, "SIX"
NumPat try7, try8, 7, "SEVEN"
NumPat try8, try9, 8, "EIGHT"
NumPat try9, 0, 9, "NINE"
NumPat try20, try30, 20, "TWENTY"
NumPat try30, try40, 30, "THIRTY"
NumPat try40, try50, 40, "FORTY"
NumPat try50, try60, 50, "FIFTY"
NumPat try60, try70, 60, "SIXTY"
NumPat try70, try80, 70, "SEVENTY"
NumPat try80, try90, 80, "EIGHTY"
NumPat try90, 0, 90, "NINETY"
include stdsets.a
dseg ends
cseg segment para public 'code'
assume cs:cseg, ds:dseg
; Semantic actions for our grammar:
;
;
;
; Get1000s- We've just processed the value one..nine, grab it from
; the value variable, multiply it by 1000, and store it
; into thousandsval.
Get1000s proc far
push ds
push dx
mov ax, dseg
mov ds, ax
mov ax, 1000
mul Value
mov ThousandsVal, ax
mov Value, 0
pop dx
mov ax, di ;Required by sl_match.
pop ds
stc ;Always return success.
ret
Get1000s endp
; Get100s- We've just processed the value one..nine, grab it from
; the value variable, multiply it by 100, and store it
; into hundredsval.
Get100s proc far
push ds
push dx
mov ax, dseg
mov ds, ax
mov ax, 100
mul Value
mov HundredsVal, ax
mov Value, 0
pop dx
mov ax, di ;Required by sl_match.
pop ds
stc ;Always return success.
ret
Get100s endp
; SetVal- This routine sets Value to whatever is in si
SetVal proc far
push ds
mov ax, dseg
mov ds, ax
mov Value, si
mov ax, di
pop ds
stc
ret
SetVal endp
; AddVal- This routine sets adds whatever is in si to Value
AddVal proc far
push ds
mov ax, dseg
mov ds, ax
add Value, si
mov ax, di
pop ds
stc
ret
AddVal endp
; Succeed matches the empty string. In other words, it matches anything
; and always returns success without eating any characters from the input
; string.
Succeed proc far
mov ax, di
stc
ret
Succeed endp
; This subroutine expects a pointer to a string containing the English
; version of an integer number. It converts this to an integer and
; prints the result.
ConvertNumber proc near
mov value, 0
mov HundredsVal, 0
mov ThousandsVal, 0
ldxi N
xor cx, cx
match
jnc NoMatch
mov al, "'"
putc
puts
print
byte "' = ", 0
mov ax, ThousandsVal
add ax, HundredsVal
add ax, Value
putu
putcr
jmp Done
NoMatch: print
byte "Illegal number",cr,lf,0
Done: ret
ConvertNumber endp
Main proc
mov ax, dseg
mov ds, ax
mov es, ax
meminit ;Init memory manager.
; Union in a "-" to the delimiters set because numbers can have
; dashes in them.
lesi delimiters
mov al, '-'
addchar
; Some calls to test the ConvertNumber routine and the conversion process.
lesi Str0
call ConvertNumber
lesi Str1
call ConvertNumber
lesi Str2
call ConvertNumber
lesi Str3
call ConvertNumber
lesi Str4
call ConvertNumber
lesi Str5
call ConvertNumber
lesi Str6
call ConvertNumber
lesi Str7
call ConvertNumber
lesi Str8
call ConvertNumber
lesi Str9
call ConvertNumber
lesi Str10
call ConvertNumber
lesi Str11
call ConvertNumber
lesi Str12
call ConvertNumber
lesi Str13
call ConvertNumber
Quit: ExitPgm
Main endp
cseg ends
sseg segment para stack 'stack'
stk db 1024 dup ("stack ")
sseg ends
zzzzzzseg segment para public 'zzzzzz'
LastBytes db 16 dup (?)
zzzzzzseg ends
end Main
Sample output:
'twenty one' = 21
'nineteen hundred thirty-five' = 1935
'thirty three thousand two hundred nineteen' = 33219
'three' = 3
'fourteen' = 14
'fifty two' = 52
'seven hundred' = 700
'two thousand seven' = 2007
'four thousand ninety six' = 4096
'five hundred twelve' = 512
'twenty three thousand two hundred ninety-five' = 23295
'seventy-five hundred' = 7500
'sixty-five thousand' = 65000
'one thousand' = 1000
- 16.8 - Some Sample Pattern
Matching Applications
- 16.8.1 - Converting Written Numbers to
Integers
Art of Assembly: Chapter Sixteen - 29 SEP 1996
[Chapter Sixteen][Previous]
[Next] [Art of
Assembly][Randall Hyde]
 zero | NonZero
zero | NonZero
zero | NonZero
Thousands Maybe100s | Hundreds Thousands
Under100 thousand Maybe100s
Hundreds |
Hundreds
Under100 hundred After100 | Under100 After100
Under100 |
Under100
Tens Maybe1s| Teens | ones Maybe1s
Ones |
ones
one | two | three | four | five | six | seven | eight | nine teens
ten | eleven | twelve | thirteen | fourteen | fifteen | sixteen | seventeen | eighteen | nineteen tens
twenty | thirty | forty | fifty | sixty | seventy | eighty | ninety